maksimum Minimum Problemleri soru çözümleri ( V ): Silindirin hacmi. ( A 300 - 2b) cdot b ). ( V' = 3456 - 528a + 12a^2 = 0 ). ( a gt 48 ) değerlerinde fonksiyon pozitif sonsuza gidiyor ve 12. ( V = 3456a - 264a^2 + 4a^3 ).
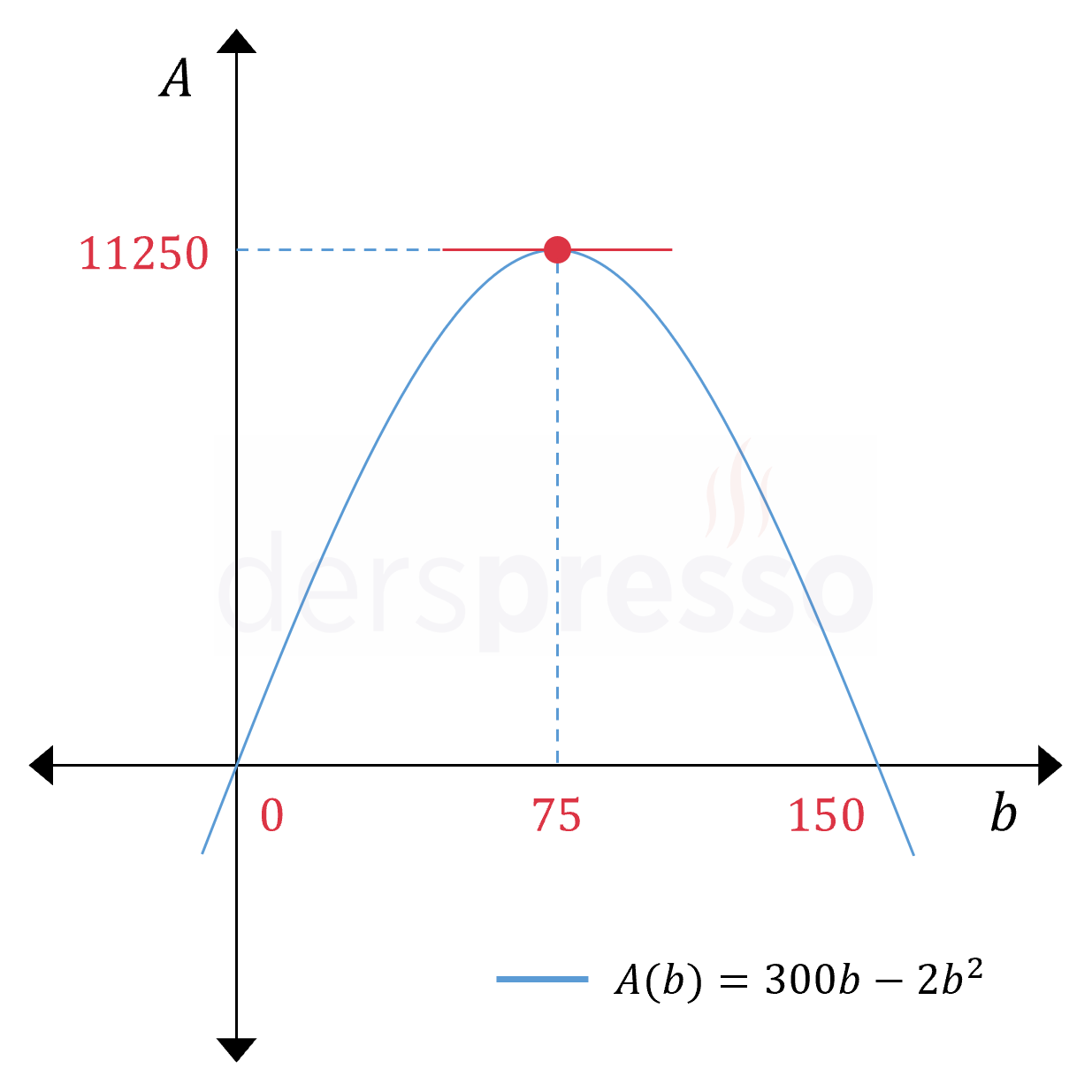
Buna göre ( alpha ) açısının ( a = 3sqrt{3} ) değerinde bir yerel ekstremum noktası vardır.
Bruh Ne Demek
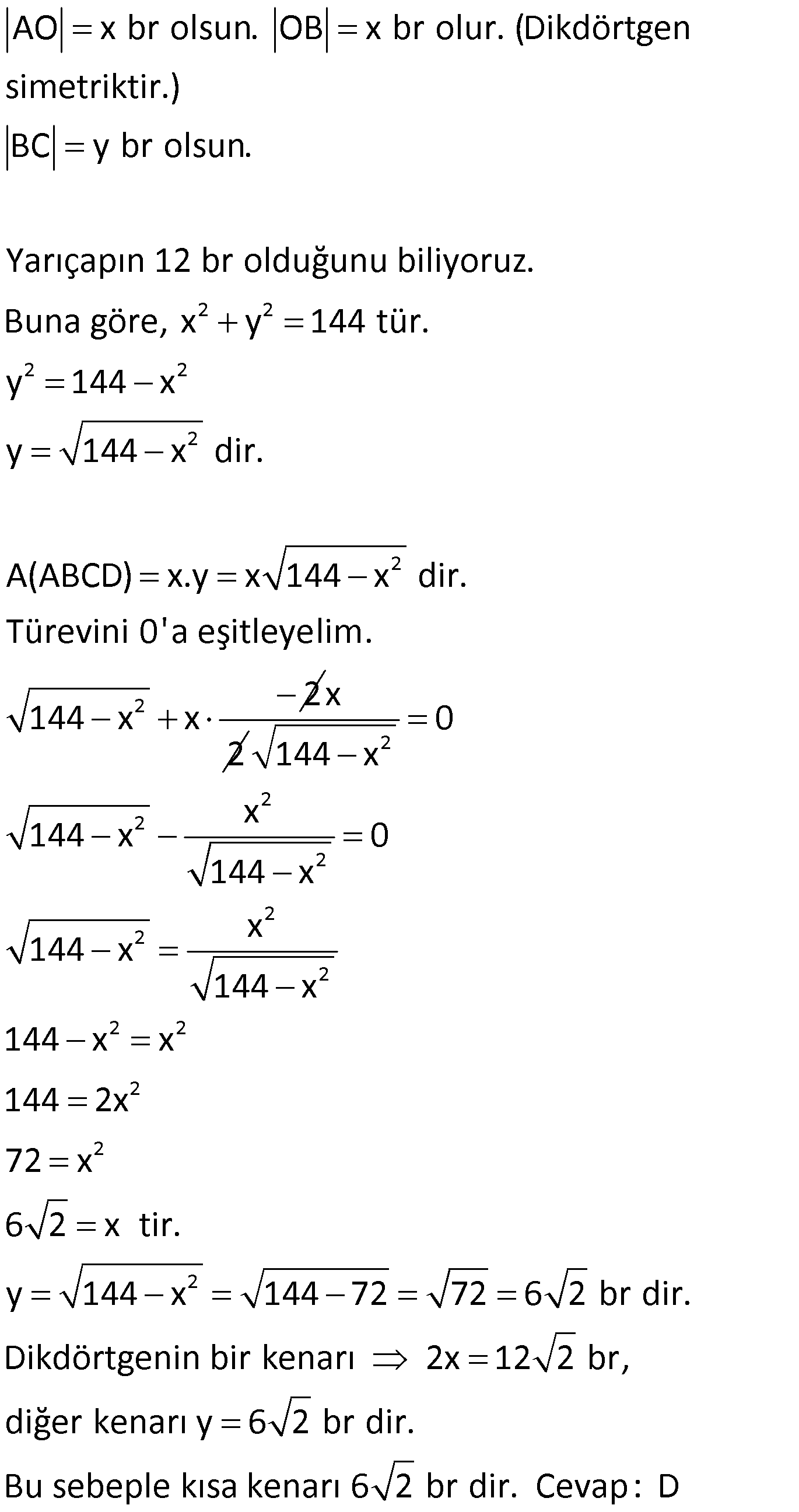
Kesilecek ( a ) uzunluğu sıfır ya da negatif olamaz, ayrıca bu uzunluk kısa kenarın uzunluğunun yarısına eşit ya da daha büyük olamaz (tüm bu durumlarda üç boyutlu bir kutu oluşmaz).
( maksimum Minimum Problemleri soru çözümleri a = 3sqrt{3} ). Birinci çarpandaki tam kare ifade sıfır ya da sıfırdan büyük olacağı için çarpan sıfıra eşit olamaz, dolayısıyla ikinci çarpanı sıfıra eşitleyebiliriz. Kartonun köşeleri kesildikten sonra geriye kalan şekildeki kenar uzunlukları yukarıdaki gibidir. Bu şeklin katlanmasıyla elde edilecek kutunun hacminin en büyük değerini bulmamız istendiği için optimize etmemiz gereken fonksiyon aşağıdaki gibidir.
Balata Nasıl Gidilir
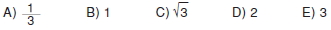
maksimum Minimum Problemleri soru çözümleri Dfrac{dfrac{6}{a}}{1 + dfrac{27}{a^2}} ). Yarıçapı 1 br olan bir kürenin içine yerleştirilebilecek en büyük hacimli dik silindirin hacmi nedir?. ( alpha ) açısı ( x ) ve ( y ) açılarının farkına eşittir.
Hızlı Bahis Giriş
Payda sıfır olamayacağı için payı sıfıra eşitleyelim. ( f'(a 12 - 3a^2 = 0 ). Bu noktanın bir ekstremum nokta olduğunu biliyor olsak da yerel minimum mu yerel maksimum mu olduğunu henüz bilmiyoruz. 300 cdot maksimum Minimum Problemleri soru çözümleri 75 - 2 cdot 75^2 ).
Beyboo

Maksimum - Minimum Problemlerinde maksimum minimum problemleri soru çözümleri uygulayabileceğimiz yöntem aşağıdaki gibidir. ( r^2 frac{h}{2})^2 = 1 ). ( f''(a -6a ).
Konu anlatımı ve soru çözümü. Problemin değişkenleri arasında tanımlı kısıtlamalar aşağıdaki gibidir:. ( b = 75 ) m.
Maksimum - Minimum Problemleri
Bahçenin alanının en büyük değerini bulmamız istendiği için optimize etmemiz gereken fonksiyon aşağıdaki gibidir. Bulduğumuz bu maksimum Minimum Problemleri soru çözümleri sonucu aşağıdaki fonksiyon grafiği üzerinden yorumlayalım. ( A(ABCD 12a - a^3 ).
( a + 2b = maksimum Minimum Problemleri soru çözümleri 300 ). ( an{x} = dfrac{9}{a}, quad an{y} = dfrac{3}{a} ). Soruda ( x ), ( y ) ve ( A ) değerleri ile ilgili ek bir kısıtlama verilmediği için üçü de tüm reel sayılarda tanımlıdır.
Şekildeki ( ABCD ) dikdörtgeninin ( [AD] ) kenarı ( y ) ekseni, ( [DC] ) maksimum Minimum Problemleri soru çözümleri kenarı ( y = 12 ) doğrusu, ( B ) köşesi de ( y = x^2 ) parabolü üzerindedir. Çözüm için Tıklayınız.
Ptt Internet Bankacılığı Açma
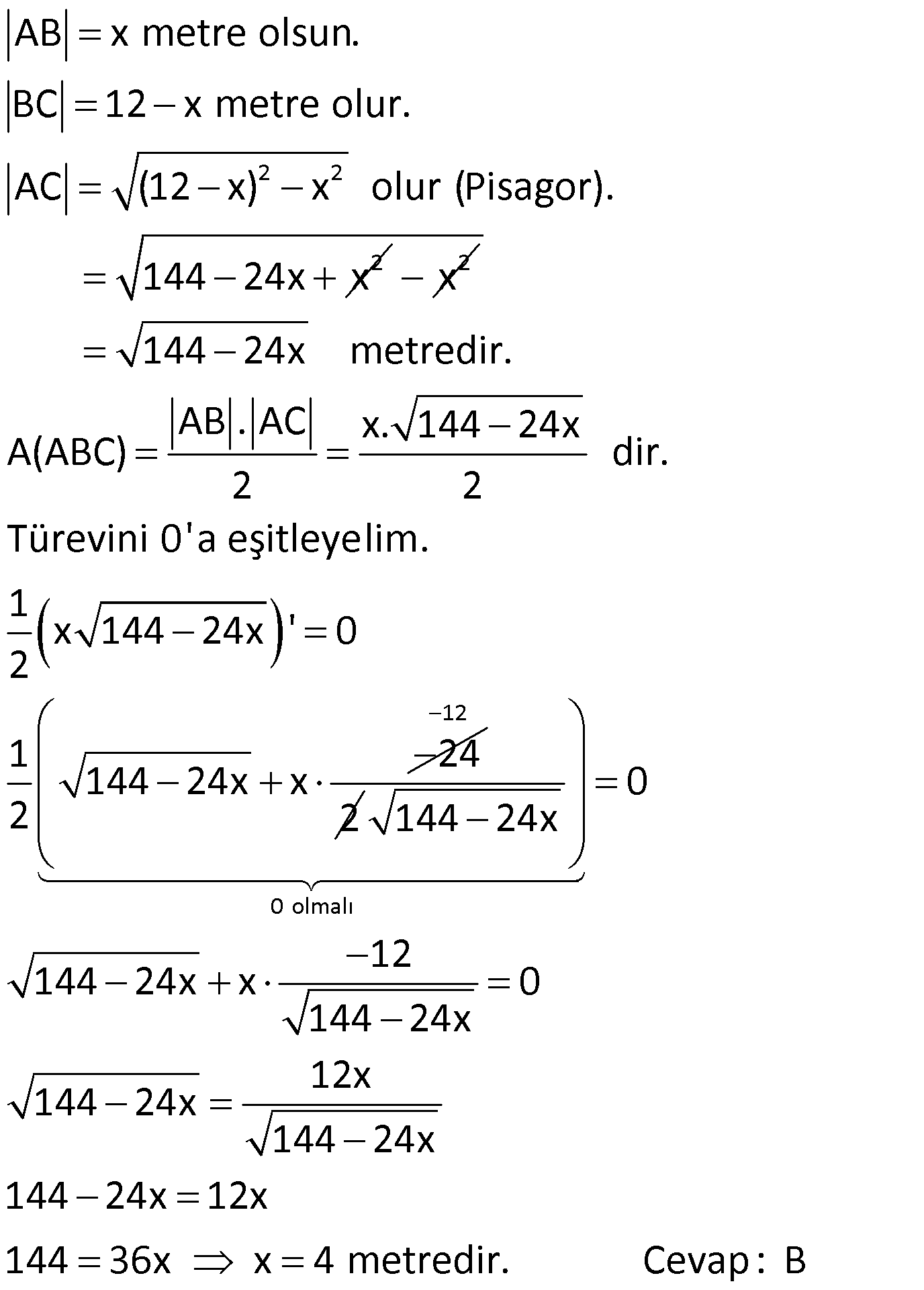
( V 96 - 2a)(36 - 2a)a ). ( x + 8y = 192 maksimum Minimum Problemleri soru çözümleri ).
Danışma Hattı